Procedural Generation with Wave Function Collapse

An In-Depth Explanation in C++, From First Principles to Practical Implementation

Wave Function Collapse (WFC) is an algorithm that has become increasingly popular for procedural generation. WFC sounds like an algorithm related to quantum mechanics, but its magic lies in something more practical: constraint solving.

What makes WFC so unique is that it can take an example image, extract a tileset from that image, and produce a new image that is similar but not identical to the input image.

Image used as example (Source: Twin Mazes)

Image progressively generated with Wave Function Collapse

This article introduces the core concepts of WFC in the following order:

1. Basic Constraint Solving — Introduces the core mechanism of WFC using a simple example of red, green, and blue tiles.

2. Bitmasks — Demonstrates how using bitwise operations can simplify constraint propagation.

3. Wang Tiles — Presents a simplified form of WFC using a simple tileset where no contradictions are possible.

4. Generating Adjacency Rules From An Input Image — Using a hash-based technique, constructs a tileset from an example image.

5. Handling Contradictions — Explains how the algorithm can detect invalid tile configurations and backtracks to recover.

6. Weighted Probability — Slightly tunes the algorithm so that it creates images that more closely resemble the input image.

With all the preliminaries out of the way, we can now examine the algorithm step by step.

---

---

Basic Constraint Solving

Suppose we want to generate a grid of red, green, and blue tiles with certain constraints. As an example, let’s say tiles of identical color cannot be placed next to each other. Under this rule, if a red tile is placed on the grid, all immediately adjacent tiles must be either green or blue.

A 5x5 grid where a red tile has been placed in the center. Each of the four adjacent tiles can only be either green or blue.

Even this simple constraint is trickier to implement than it might seem. For example, if a green tile is placed diagonally from a red tile, the tile positions that touch both the green and red tile must be set to blue.

If a green tile is placed diagonally from a red tile in the center, the tiles adjacent to both must be blue.

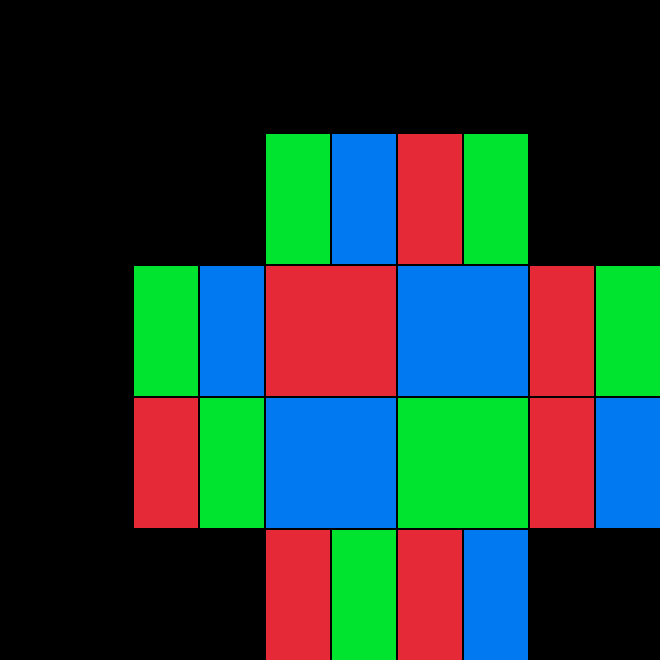
If many tiles are already placed on the board, placing a new tile might force several other tiles to become a certain color.

In this example, placing a blue tile restricts all remaining board positions to be a single color.

Constraint solving can sometimes work like a chain reaction: once a color is picked for one tile, it limits the options for the tiles that are placed next to it, which can then limit the options for the tiles that surround those tiles, and so forth.

But what does this have to do with Wave Function Collapse?

While Wave Function Collapse is typically used for procedural generation, WFC is fundamentally a constraint-solving algorithm. We can take a look at an example of how WFC would work with this 3-color tile example.

To represent the state of a given tile in the output, WFC uses one boolean for every possible color that a tile could be.

struct TilePossibilities {
  bool is_red_possible;
  bool is_green_possible;
  bool is_blue_possible;
};

A grid of these possible states is used to represent the output. When this grid is initialized, any tile can be any color, so all booleans are set to true.

constexpr U32 tiles_x = 5;
constexpr U32 tiles_y = 5;
TilePossibilities output_tile_board[tiles_x * tiles_y];

for (U32 i = 0; i < tiles_x * tiles_y; ++i) {
  output_tile_board[i] = {
    .is_red_possible = true,
    .is_green_possible = true,
    .is_blue_possible = true
  };
}

Setting a tile to a particular color means reducing all its possibilities down to one. For this example, we can set a specific tile to red. In WFC terms, this is known as collapsing a tile.

U32 x = 2;
U32 y = 2;
output_tile_board[y * tiles_x + x] = {
  .is_red_possible = true,    // tile is collapsed, only one possibility
  .is_green_possible = false,
  .is_blue_possible = false
};

Given our constraint — no tiles of identical color can touch each other — setting a tile to red means that all neighboring tiles can no longer be red. The boolean that represents the possibility of red must be set to false above, below, to the left, and to the right of the red tile.

output_tile_board[(y - 1) * tiles_x + x].is_red_possible = false;
output_tile_board[(y + 1) * tiles_x + x].is_red_possible = false;
output_tile_board[y * tiles_x + (x - 1)].is_red_possible = false;
output_tile_board[y * tiles_x + (x + 1)].is_red_possible = false;

This process is recursive. Changing a boolean in a neighboring tile might have repercussions for many other tiles on the board. This recursive constraint propagation process can be implemented with a simple flood-fill algorithm:

1. Pop position off the stack and look up its color.

2. For each cardinal direction, set boolean representing the color from step 1 to false.

3. For each tile that collapses to only one color possibility in the previous step, push its position onto the stack.

4. Repeat from step 1 until the stack is empty.

struct IndexXY {
  U32 x, y;
};

std::vector<IndexXY> stack;
stack.push_back({ x, y });

while (!stack.empty()) {
  IndexXY index = stack.back();
  stack.pop_back();

  U32 x = index.x, y = index.y;
  const TilePossibilities possibilities = output_tile_board[y * tiles_x + x];

  const auto RecursivelyPropagate = [&](U32 adjacent_x, U32 adjacent_y) {
    TilePossibilities &adjacent_tile_possibilities = output_tile_board[adjacent_y * tiles_x + adjacent_x];

    // HasTileCollapsed -> only one possible color remaining
    bool was_collapsed = HasTileCollapsed(adjacent_tile_possibilities);

    // Adjacent tiles have to be a different color from current tile
    if (HasCollapsedToRed(possibilities)) {
      adjacent_tile_possibilities.is_red_possible = false;
    }
    if (HasCollapsedToGreen(possibilities)) {
      adjacent_tile_possibilities.is_green_possible = false;
    }
    if (HasCollapsedToBlue(possibilities)) {
      adjacent_tile_possibilities.is_blue_possible = false;
    }

    // If an adjacent tile has collapsed to one color possibility,
    // it might change the color possibilities of neighboring tiles.
    bool is_collapsed = HasTileCollapsed(adjacent_tile_possibilities);
    if (!was_collapsed && is_collapsed) {
      stack.push_back({ adjacent_x, adjacent_y });
    }
  };

  if (y > 0) {
    // Up
    RecursivelyPropagate(x, y - 1);
  }
  if (y + 1 < tiles_y) {
    // Down
    RecursivelyPropagate(x, y + 1);
  }
  if (x > 0) {
    // Left
    RecursivelyPropagate(x - 1, y);
  }
  if (x + 1 < tiles_x) {
    // Right
    RecursivelyPropagate(x + 1, y);
  }
}

This simplified example is the basis of WFC:

1. Choose a tile and set it to only one possibility

2. Recursively propagate its constraints

3. Repeat until every tile on the board only has one possibility

This example used only three different types of tiles and one simple constraint for how tiles can be placed together. Real tilesets, however, often have many more tiles with more complicated rules for how tiles can be placed.

Using Bitmasks To Represent Possible Tiles

WFC requires one bit for each possible state of every tile in the output. These states can be compactly stored in bitmasks.

Using the example from the previous section, each tile needs 3 bits to store each color.

enum TileColor {
  Red = 1 << 0,   // Bit 0 - red
  Green = 1 << 1, // Bit 1 - green
  Blue = 1 << 2   // Bit 2 - blue
};

U32 output_tile_board[tiles_x * tiles_y];

Bitmasks simplify the constraint-solving code because bitwise operators correspond to logical set operations. For example, the initial state of the output grid is that all tiles can be any color — i.e., they can be red, green, or blue. If each color is represented by a single bit, setting all 3 bits to true means any color is valid.

for (U32 i = 0; i < tiles_x * tiles_y; ++i) {
  // a tile can be red, green, or blue
  U32 tile_possibilities = TileColor::Red | TileColor::Green | TileColor::Blue;
  output_tile_board[i] = tile_possibilities;
}

The number of bits set in the bitmask corresponds to the number of possibilities remaining at that tile position. Counting the number of bits in a bitmask can be done easily with the popcount intrinsic.

#include <bit>
// ...
U32 remaining_possibilities = std::popcount(output_tile_board[index]);
bool is_tile_collapsed = remaining_possibilities == 1;

If a tile is red, the tiles surrounding it must not be red. With bitmasks, this means clearing the red bit in all the adjacent tiles.

output_tile_board[y * tiles_x + x] = TileColor::Red;

// Set red bit to false in neighboring tiles
output_tile_board[(y - 1) * tiles_x + x] &= ~(TileColor::Red);
output_tile_board[(y + 1) * tiles_x + x] &= ~(TileColor::Red);
output_tile_board[y * tiles_x + (x - 1)] &= ~(TileColor::Red);
output_tile_board[y * tiles_x + (x + 1)] &= ~(TileColor::Red);

Bitmasks also allow us to easily scale to a larger number of tile possibilities and keep the representation of data very compact.

Using WFC With A Simple Tileset

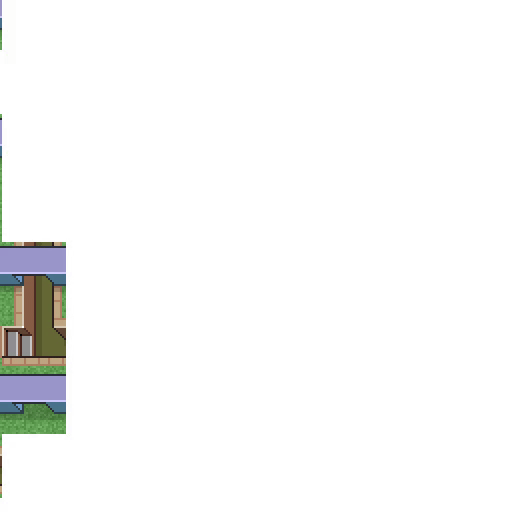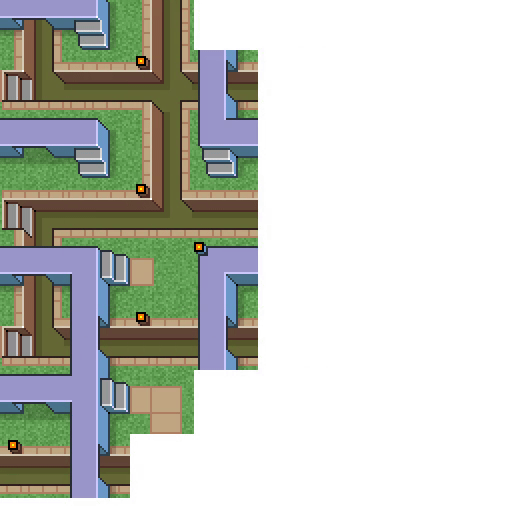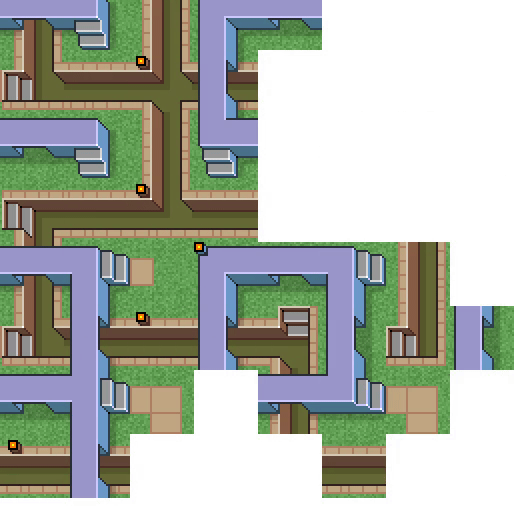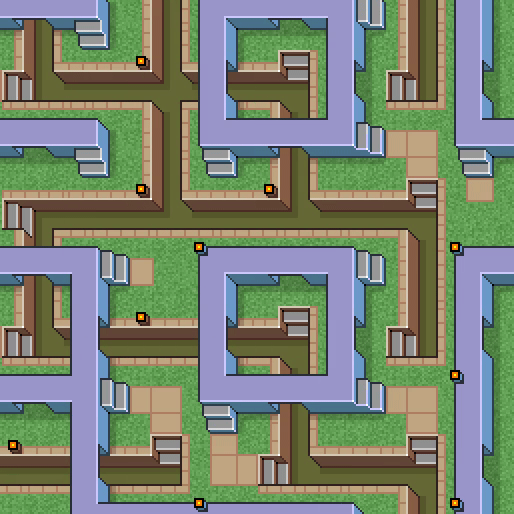
In practice, most tilesets are considerably more elaborate than simple color patterns. They often require tiles to be arranged in a specific way to produce a coherent, continuous image. This section examines 2-edge Wang Tiles and how they can be used with Wave Function Collapse.

Example of 2-edge pipe tileset

2-edge Wang Tiles form labyrinth-like patterns when placed on a grid. Each square tile can either connect or not connect on each of its four sides. Tiles can only be placed next to each other if their touching edges match. In the example above, a pipe going to the right has to connect to a pipe coming from the left.

A right-facing tile placed next to a left-facing tile. Both tiles are connected on one side and unconnected on their three other sides.

A complete tileset includes all combinations of connected and unconnected edges on each of its four sides.

The complete 2-edge pipe tileset (16 tiles)

This tileset is structured in a specific way that makes it easy to compute which directions each pipe is facing. Each tile’s index, counting from left to right, is a 4-bit mask, where each bit indicates a connection in one direction:

• Bit 0 set → connected up

• Bit 1 set → connected right

• Bit 2 set → connected down

• Bit 3 set → connected left

For example, tile 5 is a vertical pipe that is connected up and down.

5 is represented as 0b0101 in binary, which has both bit 0 and bit 2 set.

Combining 5 with bit 1 using a bitwise OR (0b0101 | 0b0010 = 0b0111) gives 7, the index of the tile that connects upward, downward, and to the right.

The structure of this tileset makes it possible to compute an adjacency ruleset for all tiles very quickly. Each tile needs a ruleset with 16 bits per direction, where each bit indicates whether a given tile can be placed next to the current one.

struct AdjacencyRuleset {
  U16 up, down, right, left;
};

As an example, we can manually fill out the AdjacencyRuleset struct for tile 3:

Tile 3 depicts a pipe segment that connects upward and to the right. It can’t connect to another pipe downward, nor can it connect to the left.

The adjacency ruleset for tile 3 should reflect these constraints:

1. Any tile connecting downward can be placed above tile 3

2. Any tile connecting to the left can be placed to the right of tile 3

3. If a tile is not connected to the right, it can be placed to the left of tile 3

4. If a tile is not connected upward, it can be placed below tile 3

AdjacencyRuleset tile_3_ruleset = { 0, 0, 0, 0 };

for (U32 i = 0; i < 16; ++i) {
  bool connects_up    = (i & 0x1) != 0;
  bool connects_right = (i & 0x2) != 0;
  bool connects_down  = (i & 0x4) != 0;
  bool connects_left  = (i & 0x8) != 0;

  // A tile above must connect downward
  if (connects_down) {
    tile_3_ruleset.up |= 1u << i;
  }

  // A tile to the right must connect left
  if (connects_left) {
    tile_3_ruleset.right |= 1u << i;
  }

  // A tile to the right must NOT connect right
  if (!connects_right) {
    tile_3_ruleset.left |= 1u << i;
  }

  // A tile below must NOT connect upward
  if (!connects_up) {
    tile_3_ruleset.down |= 1u << i;
  }
}

This can be generalized to work with any tile. First, we’ll create four bitmasks that represent all tiles that connect in each direction.

U16 all_tiles_connecting_up = 0;
U16 all_tiles_connecting_right = 0;
U16 all_tiles_connecting_left = 0;
U16 all_tiles_connecting_down = 0;

for (U32 i = 0; i < 16; ++i) {
  bool tile_connects_up    = (i & 0x1) != 0;
  bool tile_connects_right = (i & 0x2) != 0;
  bool tile_connects_down  = (i & 0x4) != 0;
  bool tile_connects_left  = (i & 0x8) != 0;

  if (tile_connects_up) {
    all_tiles_connecting_up |= 1 << i;
  }
  if (tile_connects_right) {
    all_tiles_connecting_right |= 1 << i;
  }
  if (tile_connects_down) {
    all_tiles_connecting_down |= 1 << i;
  }
  if (tile_connects_left) {
    all_tiles_connecting_left |= 1 << i;
  }
}

Because this is a 2-edge tileset, each side of a tile can either be connected or unconnected. That duality means every connection has an inverse: if a tile has a connection to the right side, it can only connect to the left of a left-connecting tile. Exactly half of the tiles (8 of 16) connect left, and the other half do not. The same logic applies to every direction.

This natural symmetry can be exploited when computing a bitmask for any tile. If a tile has an upward connection, its up bitmask is the set of all tiles that connect downward. If it does not have an upward connection, the up bitmask is the set of all tiles that do not connect downward — the exact bitwise inverse of the downward set.

bool tile_connects_up    = (tile_index & 0x1) != 0;
bool tile_connects_right = (tile_index & 0x2) != 0;
bool tile_connects_down  = (tile_index & 0x4) != 0;
bool tile_connects_left  = (tile_index & 0x8) != 0;

AdjacencyRuleset ruleset = {};

// By symmetry: if a side is connected, allow neighbors that connect back
// If a side is unconnected, allow neighbors that are also unconnected
if (tile_connects_up) {
  // Above: must connect downward
  ruleset.up = all_tiles_connecting_down;
} else {
  // Below: must NOT connect downward
  ruleset.up = ~all_tiles_connecting_down;
}

if (tile_connects_right) {
  ruleset.right = all_tiles_connecting_left;
} else {
  ruleset.right = ~all_tiles_connecting_left;
}

if (tile_connects_down) {
  ruleset.down = all_tiles_connecting_up;
} else {
  ruleset.down = ~all_tiles_connecting_up;
}

if (tile_connects_left) {
  ruleset.left = all_tiles_connecting_right;
} else {
  ruleset.left = ~all_tiles_connecting_right;
}

The code above computes the ruleset for a single tile, but in WFC, each grid cell may hold multiple tile possibilities. If any potential tile at a given position has a connection up, that means any tile that has a connection down can be placed above it. If this position does not have a connection, the tile above it must also be unconnected. If it’s possible to place both upward-connecting tiles and tiles that don’t connect upward at the same position, any tile can be placed above it. This rule is true for any direction.

// Compute adjacency ruleset for any possible tile
AdjacencyRuleset ComputeAdjacencyRuleset(U16 possible_tiles) {
  AdjacencyRuleset result = {};

  // if any possible tile connects up, tiles above can connect down
  if ((possible_tiles & tiles_connecting_up) != 0) {
    result.up |= all_tiles_connecting_down;
  }

  // if any possible tile does not connect up, tiles above can be unconnected down
  if ((possible_tiles & ~tiles_connecting_up) != 0) {
    result.up |= ~all_tiles_connecting_down;
  }

  // same for left, right, and down

  return result;
}

Once the adjacency rulesets have been defined, WFC can run its constraint propagation loop.

The remainder of this section will implement a simplified form of WFC:

1. Randomly choose a position in the 2D grid

2. Collapse it to one possibility: set all possibilities to false, except for one

3. Push the collapsed position onto a stack.

4. Pop position off the stack.

5. Compute the adjacency ruleset for all tile possibilities in each direction from that position.

6. Bitwise AND the possible tiles in the ruleset with possibilities stored in the 2D output grid. If any stored possibility bitmasks in adjacent positions change in the process of doing this, push them onto the stack.

7. If the stack is not empty, go back to step 4.

The first step is to choose a grid position to collapse. This randomly chosen position must have more than one tile that can be placed there.

std::vector<IndexXY> positions_to_choose_from;

for (U32 y = 0; y < tiles_y; ++y) {
  for (U32 x = 0; x < tiles_x; ++x) {
    U16 tile_possibilities = output_tile_board[y * tiles_x + x];
    U16 number_of_possible_tiles = std::popcount(tile_possibilities);
    if (number_of_possible_tiles > 1) {
      positions_to_choose_from.push_back({ x, y });
    }
  }
}

U32 size = positions_to_choose_from.size();
if (size == 0) {
  // algorithm is already done
  return;
}
IndexXY random_index = positions_to_choose_from[RandomInt() % size];

At the chosen grid position, one of the tile possibilities is selected. In bitmask form, this means randomly picking from one of the set bits.

// Naïve random bit select
U16 RandomlySelectPossibility(U16 possibilities) {
  std::vector<U32> tiles;

  for (U32 i = 0; i < 16; ++i) {
    if ((possibilities & (1ull << i)) != 0) {
      tiles.push_back(i);
    }
  }

  U32 random_index = RandomInt() % tiles.size();
  return 1ull << tiles[random_index];
}

// Efficient random bit select on x64 - not portable
U16 RandomlySelectPossibility(U16 possibilities) {
  U32 popcount = std::popcount(possibilities);
  U64 bit_index = 1ull << (RandomInt() % popcount);
  U64 collapsed_tile = _pdep_u64(bit_index, possibilities);
  return (U16)collapsed_tile;
}

Once a random bit is selected, all other bits are set to false, and the new value is stored in the output.

U16 tile_possibilities = output_tile_board[selected_tile_index];
U16 collapsed_tile = RandomlySelectPossibility(tile_possibilities);
// collapsed_tile only has 1 bit enabled
output_tile_board[selected_index] = collapsed_tile;

After collapsing a tile, the constraints must be recursively propagated outward. This can be done with a flood-fill algorithm.

void PropagateConstraints(U32 x, U32 y) {
  std::vector<IndexXY> stack;
  stack.push_back({ x, y });
  while (!stack.empty()) {
    IndexXY index = stack.back();
    stack.pop_back();

    auto RecursivelyPropagate = [&](U32 x, U32 y, U16 adjacent_tile_mask) {
      U16 tile_possibilities = output_tile_board[y * tiles_x + x];
      U16 masked_tile_possibilities = tile_possibilities & adjacent_tile_mask;

      if (tile_possibilities != masked_tile_possibilities) {
        output_tile_board[y * tiles_x + x] = masked_tile_possibilities;
        stack.push_back({ x, y });
      }
    };

    U32 x = index.x, y = index.y;
    U16 tile_possibilities = output_tile_board[y * tiles_x + x];

    auto valid_adjacent_tiles = ComputeAdjacencyRuleset(tile_possibilities);

    if (y > 0) {
      RecursivelyPropagate(x, y - 1, valid_adjacent_tiles.up);
    }
    if (y + 1 < tiles_y) {
      RecursivelyPropagate(x, y + 1, valid_adjacent_tiles.down);
    }
    if (x > 0) {
      RecursivelyPropagate(x - 1, y, valid_adjacent_tiles.left);
    }
    if (x + 1 < tiles_x) {
      RecursivelyPropagate(x + 1, y, valid_adjacent_tiles.right);
    }
  }
}

Once this is implemented correctly, we get an algorithm that looks like this:

Simplified WFC for Wang Tiles: collapse and propagate until the board is fully resolved. Each time a tile is chosen, there are fewer possible tiles that can be placed in adjacent tiles.

A complete 2-edge Wang tileset makes a constraint-solving algorithm easier to implement: regardless of which tiles are chosen or in what order, there will always be at least one valid tile for every grid position.

The full WFC algorithm, however, is more general. It can generate new images by learning patterns from an input example, where the tileset isn’t known ahead of time and may be incomplete. The remainder of this article will focus on using WFC in this context.

Generating Adjacency Rules From An Input Image

Instead of using predetermined adjacency rules, they can be implicitly determined from an image with examples of how that tileset is used. To do this, WFC takes the following approach:

1. Load an image to be used as an example

2. Choose an NxN size

3. Scan all NxN regions from the source image

   1. Hash the pixel contents of each NxN region

   2. The hash is used to uniquely identify tiles and find duplicates

   3. Assign a unique identifier to each distinct tile (e.g., 0 for the first NxN region, 1 for the second unique NxN region, 2 for the third, and so on)

4. Create a 2D array of tile identifiers

   1. Each entry in the array corresponds to a position in the source image and records which unique NxN tile appears there

   2. This structure makes it easy to determine which tiles are adjacent in the source image

5. For each tile identifier, create 4 bitmasks that represent the valid tiles that can be placed in each cardinal direction.

   1. Initialize them all to 0.

6. Iterate through the 2D tile identifier array and compute adjacency rulesets.

   1. Find the 4 bitmasks that correspond to the tile identifier.

   2. For each neighboring tile, mark it as valid in the corresponding adjacency bitmask by setting the bit at the neighbor’s tile identifier (1 << neighbor_id).

The first step is to choose an image to be used as an example.

Image image = LoadImage("example.png");

Deciding an NxN region size is somewhat arbitrary and will depend on the input image. Once it has been decided, the first step is to iterate over each NxN region and compute a hash to uniquely identify its contents.

The following is an example that computes a 64-bit hash per 32x32 region:

constexpr U32 tile_size = 32; // NxN region size

// iterate over all 32x32 regions in source image
for (U32 y = 0; y < tiles_y; ++y) {
  for (U32 x = 0; x < tiles_x; ++x) {
    U64 hash = 0x1;

    // compute hash for 32x32 region
    for (U32 local_y = 0; local_y < tile_size; ++local_y) {
      for (U32 local_x = 0; local_x < tile_size; ++local_x) {
        U32 region_left = x * tile_size;
        U32 region_top  = y * tile_size;
        U32 absolute_x = region_left + local_x;
        U32 absolute_y = region_top + local_y;
        U32 index = absolute_y * image.width + absolute_x;

        U8 *data = (U8 *)image.data;
        U8 r = data[index * 3 + 0];
        U8 g = data[index * 3 + 1];
        U8 b = data[index * 3 + 2];

        // basic pixel-based hash
        hash *= 0xCE2273B48A5DA531ULL;
        U64 combined_color = Xorshift64((((U64)r << 16) | ((U64)g << 8) | b) * 0x3CEAE4A956524891ULL);
        hash ^= combined_color;
      }
    }
    // ...

If the input image contains fewer than 64 unique tiles, the adjacency rules can be represented with 64-bit bitmasks. To do this, each unique NxN region hash must be mapped to a compact identifier in the range [0, 64).

This mapping can be done with a hashmap: the key is the 64-bit region hash, and the value is a sequential ID assigned to each new tile when it is discovered. The result is a dense set of tile identifiers (0, 1, 2, 3, …) that can be used easily with bitmasks.

These identifiers are stored in a 2D array, where each entry corresponds to a tile in the input image.

std::unordered_map<U64, U32> map = {};
U32 unique_tile_count = 0;
U32 tile_board[max_tile_count];

for (U32 y = 0; y < tiles_y; ++y) {
  for (U32 x = 0; x < tiles_x; ++x) {
    U64 hash = 0x1;
    // compute hash for 32x32 region
    // ...
    
    U32 tile_id;
    if (!map.contains(hash)) {
      tile_id = unique_tile_count++;
      map[hash] = tile_id;
    } else {
      tile_id = map[hash];
    }
    tile_board[y * tiles_x + x] = tile_id;
  }
}

After filling out the entire 2D unique identifier array, it’s very easy to compute adjacency rulesets for each tile. Simply iterate over every tile, look in each direction, and set adjacent tiles as valid in their corresponding bitmasks.

struct AdjacencyRuleset {
  U64 up, down, right, left;
};

U32 max_tile_count = 64;
AdjacencyRuleset constraints[max_tile_count];

for (U32 y = 0; y < tiles_y; ++y) {
  for (U32 x = 0; x < tiles_x; ++x) {
    U32 tile_id = input_tile_ids[y * tiles_x + x];

    {
      // toroidal wraparound
      U32 y_up = (y != 0) ? y - 1 : tiles_y - 1;
      U32 top_tile_id = tile_board[y_up * tiles_x + x];

      constraints[tile_id].up |= 1ull << top_tile_id;
      constraints[top_tile_id].down |= 1ull << tile_id;
    }

    // same logic for left, right, and down...
  }
}

To compute an adjacency ruleset for an output position with multiple tile possibilities, the simplest approach is to iterate over all tile possibilities, find their precomputed adjacency ruleset, and bitwise OR them all together.

AdjacencyRuleset ComputeAdjacencyRuleset(U64 possibilities) {
  AdjacencyRuleset result = {};

  while (possibilities) {

    // Look at one tile id
    U64 tile_id = std::countr_zero(possibilities);

    // Find its adjacency ruleset
    AdjacencyRuleset valid_neighbors = constraints[tile_id];

    // OR it with all other possible tile adjacency rulesets
    result.up |= valid_neighbors.up;
    result.down |= valid_neighbors.down;
    result.right |= valid_neighbors.right;
    result.left |= valid_neighbors.left;

    // clear tile bit, advance loop
    possibilities &= ~(1ull << tile_id);
  }

  return result;
}

At this point, the adjacency rules have been extracted directly from the source image. The rest of the Wave Function Collapse logic covered up to this point (collapsing, constraint propagation, etc.) remains exactly as described earlier. However, there is one caveat: a source image might have a very complicated set of tiles that can only be placed together in specific ways. During the collapse and propagation process, tiles might be placed in a way that’s incompatible with the adjacency ruleset. This will be the focus of the next section.

Handling Contradictions

When generating an image from more complicated tilesets, the algorithm can run into pathological cases, where collapsing a tile causes the resulting board to be in an invalid state. In WFC terms, this invalid state is called a contradiction.

Example of constraint propagation loop generating an invalid tile configuration

Fortunately, detecting a contradiction is straightforward: if at any point during the constraint propagation process, a position in the output has 0 remaining possibilities, a mistake has occurred somewhere, and the algorithm has to backtrack.

Resolving a contradiction requires undoing the decision that caused the contradiction. The simplest way to achieve this is by storing which tile positions have been collapsed, what possibilities haven’t been tried yet, and the entire state of the board at the time of collapsing a tile. There are more memory-efficient ways to handle a contradiction, but for small outputs, this is perfectly fine.

struct UndoEntry {
  IndexXY index;
  U64 untried_possibilities;
  U64 previous_board_state[tiles_x * tiles_y];
};

std::vector<UndoEntry> undo_stack;

U64 collapsed_tile = CollapseTile(tile_possibilities);

UndoEntry entry = {
  .index = selected_tile.index,
  .untried_possibilities = tile_possibilities & ~collapsed_tile,
  .previous_board_state = {}
};

// Copy entire state of the board in case we need to revert
memcpy(
  (void *)entry.previous_board_state,
  (void *)output_tile_board,
  sizeof(output_tile_board)
);

undo_stack.push_back(entry);

U32 flat_index = selected_tile.index.y * tiles_x + selected_tile.index.x;
output_tile_board[flat_index] = collapsed_tile;

Next, the constraint propagation loop should detect when a contradiction has occurred.

void PropagateConstraints(U32 x, U32 y) {
  std::vector<IndexXY> stack;
  stack.push_back({ x, y });

  bool has_contradiction_occurred = false;
  while (!stack.empty() && !has_contradiction_occurred) {
    IndexXY index = stack.back();
    stack.pop_back();

    auto RecursivelyPropagate = [&](U32 x, U32 y, U64 adjacent_tile_mask) {
      U16 tile_possibilities = output_tile_board[y * tiles_x + x];
      U16 masked_tile_possibilities = tile_possibilities & adjacent_tile_mask;

      if (masked_tile_possibilities == 0) {
        has_contradiction_occurred = true;
        return;
      }

      if (tile_possibilities != masked_tile_possibilities) {
        output_tile_board[y * tiles_x + x] = masked_tile_possibilities;
        stack.push_back({ x, y });
      }
    };

    // compute adjacency ruleset for current tile

    // recursively propagate up, down, left, and right
  }

If the constraint propagation loop detects a contradiction, the state of the board must be reverted, and a different tile must be selected. Ideally, another contradiction won’t happen as a result of this new tile decision, but if another contradiction occurs, the reversion process must continue until a tile can be placed without causing a contradiction.

Example of Wave Function Collapse undoing a change that caused a contradiction

// if all possibilities have been exhausted for current position,
// pop off the undo stack
while (!undo_stack.empty() && undo_stack.back().untried_possibilities == 0) {
  undo_stack.pop_back();
}

if (undo_stack.empty()) {
  // it's impossible to generate an image using this tileset
  return;
}

UndoEntry &entry = undo_stack.back();

// restore state of the board
memcpy(
  (void *)output_tile_board,
  (void *)entry.previous_board_state,
  sizeof(output_tile_board)
);

// try collapsing a different tile
U64 collapsed_tile = CollapseTile(entry.untried_possibilities);

// remember which tiles haven't been tried in case more contradictions occur
entry.untried_possibilities &= ~collapsed_tile;
selected_tile.index = entry.index;
output_tile_board[entry.index.y * tiles_x + entry.index.x] = collapsed_tile;

// propagate constraints from newly selected tile
constraint_propagation_stack.clear();
constraint_propagation_stack.push_back(entry.index);

Although the algorithm developed up to this point is completely capable of generating a valid, continuous image using tiles from an example image, it won’t fully capture the style of the source image. If every tile is chosen with equal probability, the output will be structurally consistent but statistically off: tiles that appear frequently in the source image will show up just as often as ones that appear only once. The solution is to weight tiles by their frequency in the input, which is the focus of the next section.

Weighted Probability

When deciding which tiles to place, the Wave Function Collapse algorithm weights the probability of each tile according to how often it appears in the source image. This is an easy-to-compute heuristic that significantly improves the quality of the output.

In order to compute weighted probabilities, the frequency of each tile must be counted. This can be added to the tile hashing code described in the previous section.

U32 tile_counts[max_tile_count];

// compute hash for NxN

U32 tile_id;
if (!map.contains(hash)) {
  tile_id = unique_tile_count++;
  map[hash] = tile_id;

  // first occurrence - set count to 1
  tile_counts[tile_id] = 1;
} else {
  tile_id = map[hash];

  // duplicate occurrence - add 1 to existing count
  tile_counts[tile_id] += 1;
}

Next, when collapsing a tile, each possible tile should be weighted according to its distribution in the input image.

struct ProbabilityWeight {
  U32 low;
  U32 high;
  U32 tile;
};

// Brute-force weighted probability
U64 CollapseTile(U64 possibilities) {
  std::vector<ProbabilityWeight> probabilities;
  probabilities.reserve(std::popcount(possibilities));

  // For every set bit, push a weight proportional to its count
  // count occurrences of all potential tiles
  U32 current_count = 0;
  for (U32 i = 0; i < 64; ++i) {
    U64 tile_bit = 1ull << i;
    if ((possibilities & tile_bit) != 0) {
      U32 weight = tile_counts[i];
      ProbabilityWeight w = { current_count, current_count + weight - 1, i };
      probabilities.push_back(w);
      current_count += weight;
    }
  }

  // randomly select a value: [0, occurrences of all potential tiles)
  U32 random_value = RandomInt(&random_state) % current_count;
  U32 collapsed_tile;

  // find which tile corresponds to randomly selected value
  for (U32 i = 0; i < probabilities.size(); ++i) {
    ProbabilityWeight weight = probabilities[i];
    if (random_value >= weight.low && random_value <= weight.high) {
      collapsed_tile = weight.tile;
      break;
    }
  }

  return 1ull << collapsed_tile;
}

This simple change biases the distribution of tiles in the output to reflect that of the input image.

Weighted probabilities can also be used to improve the order in which tiles are collapsed, which reduces the amount of backtracking the algorithm has to do.

Wave Function Collapse uses Shannon entropy as a heuristic for which tile to collapse next.

\(-\sum_{i=1}^{n} p_i \,\log_2 p_i\)

A tile position’s Shannon entropy decreases as its possibilities shrink, so the position with the lowest entropy is the one with the least uncertainty about what can go there.

To compute a position’s Shannon entropy, we start by summing the counts of all valid tiles at that location.

U64 tile_possibilities = output_tile_board[index];

F64 tile_count_in_input_image = 0.0;
while (tile_possibilities) {
  // find one valid tile that can be placed at this location
  U64 tile_id = std::countr_zero(tile_possibilities);

  // add its count to the total count
  tile_count_in_input_image += (F64)tile_counts[tile_id];

  // clear bit representing tile, advancing to next tile on next iteration
  tile_possibilities &= ~(1ull << tile_id);
}

These counts are then normalized into probabilities, and the entropy is obtained by multiplying that probability by the logarithm of itself.

tile_possibilities = output_tile_board[index];
F64 computed_entropy = 0.0;
while (tile_possibilities) {
  // find one valid tile that can be placed at this location
  U64 tile_id = std::countr_zero(tile_possibilities);

  // find its count
  F64 tile_count = (F64)tile_counts[tile_id];

  // normalize count into probability
  F64 probability = tile_count / tile_count_in_input_image;

  // multiply probability with its own logarithm
  // subtract from total entropy from this tile position
  computed_entropy -= probability * std::log2(probability);

  // clear bit representing tile, advancing to next tile on next iteration
  tile_possibilities &= ~(1ull << tile_id);
}

To find the position with the lowest entropy, we can simply compute the entropy for each position in the 2D grid and take the minimum. If multiple tile positions end up with the same minimum entropy, we can tie-break by selecting randomly between them.

F64 lowest_entropy = DBL_MAX;
std::vector<IndexXY> low_entropy_positions;

for (U32 y = 0; y < tiles_y; ++y) {
  for (U32 x = 0; x < tiles_x; ++x) {

    U64 tile_possibilities = output_tile_board[y * tiles_x + x];

    // skip if position has already been collapsed to one possibility
    if (std::popcount(tile_possibilities) <= 1) {
      continue;
    }

    F64 computed_entropy = 0.0;

    // ...
    // compute tile entropy
    // ...

    if (computed_entropy < lowest_entropy) {
      lowest_entropy = computed_entropy;
      low_entropy_positions.clear();
      low_entropy_positions.push_back({ x, y });
      continue;
    }

    if (computed_entropy == lowest_entropy) {
      low_entropy_positions.push_back({ x, y });
    }
  }
}

U32 index_count = low_entropy_positions.size();
if (index_count != 0) {
  U32 random_index = RandomInt() % index_count;
  U32 selected_tile_position = low_entropy_positions[random_index];
  // ...

With these simple changes, the algorithm doesn’t just generate valid outputs—it produces patterns that statistically echo the source image while avoiding contradictions.

Conclusion

This article demonstrated all the major concepts of WFC: boolean states, constraint propagation, entropy calculation, and backtracking. To recap, WFC is defined by the following steps:

1. Extract tileset from image. Use an image as an example for procedural generation and partition it into NxN regions. Each distinct region becomes a tile. Record which tiles occur adjacent to each other in the four cardinal directions.

2. Initialize output grid. Each cell of the grid begins as a set of booleans, one per tile found in the input image, all initially true. Each boolean represents a possible tile that can be placed at that cell.

3. Select a cell. From all cells with more than one remaining tile possibility, choose the one with the lowest Shannon entropy. If the grid has more than one cell with the same low entropy, break the tie randomly.

4. Collapse the cell. Randomly select one of its valid tiles, weighted by frequency in the input. Set the boolean representing the tile to true, while setting all others to false.

5. Propagate constraints. Apply the adjacency rules outward: eliminate incompatible tiles from neighboring cells. Continue recursively until no further eliminations are possible.

6. Handle contradictions. If any cell gets to a point where there are no longer any valid tiles (all booleans set to false), revert to a prior state and try a different tile.

7. Iterate. Repeat steps 3–6 until every cell in the grid has collapsed to exactly one tile.

While the version here is complete and functional, it is only a starting point. There are many things that can be tweaked when implementing WFC in practice: incorporating tile rotations and reflections, experimenting with different region sizes, and combining WFC with other procedural generation techniques.

---